排序

# 插入排序

# 直接插入排序

直接插入排序

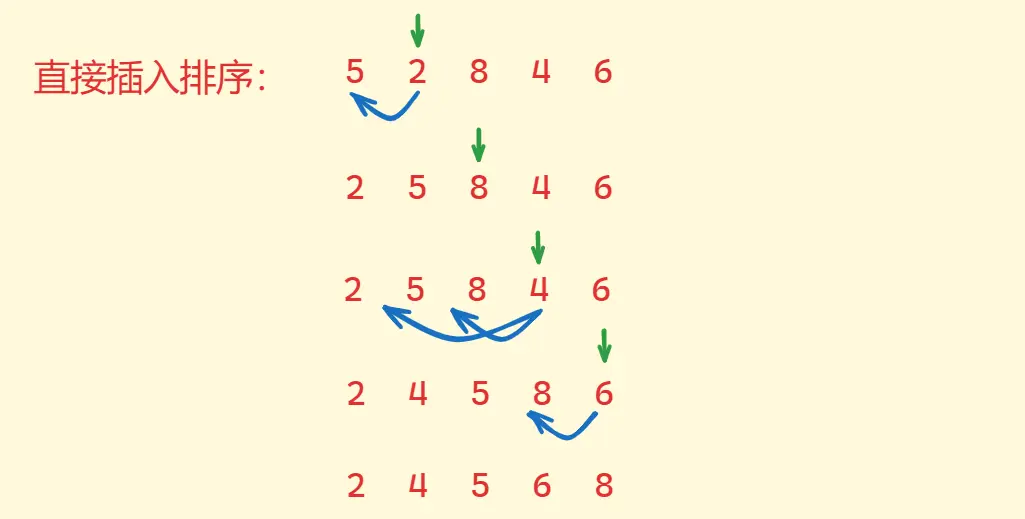
void InsertSort() {
    if (nums.size() <= 1)
        return;
    for (int i = 1; i < nums.size(); i++) {
        int j = i;
        // 因为前面已经有序
        while (j >= 0 && nums[j] < nums[j - 1]) {
            swap(nums[j], nums[j - 1]);
            j--;
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12

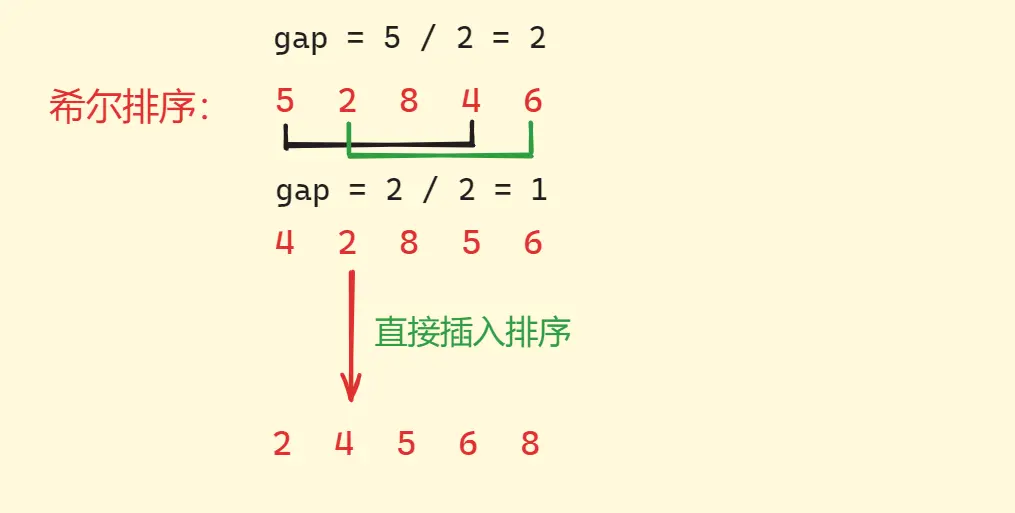
# 希尔排序

对直接插入排序的优化

预排序：按照一个间距 gap进行排序
直接插入排序

gap 越大，前面大的数可以越快到后面，后面小的数可以越快到前面，越不接近有序。

希尔排序

void ShellSort() {
    int gap = nums.size();
    while (gap > 0) {
        gap /= 2;
        for (int i = 0; i < nums.size(); i++) {
            int j = i;
            while (j - gap >= 0 && nums[j] < nums[j - gap]) {
                swap(nums[j], nums[j - gap]);
                j -= gap;
            }
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13

# 选择排序

每次从待排序列中选出一个最小值，然后放在序列的起始位置，直到全部待排数据排完即可。

void SelectSort_single() {
    for (int i = 0; i < nums.size(); i++) {
        int min = i;
        for (int j = i; j < nums.size(); j++) {
            if (nums[j] < nums[min]) {
                min = j;
            }
        }
        swap(nums[i], nums[min]);
    }
}

1
2
3
4
5
6
7
8
9
10
11

为了提高效率，每次从待排序列中选出一个最小值和一个最大值，直到全部待排数据排完即可。

void SelectSort_double() {
    int min = 0;
    int max = nums.size() - 1;
    while (min < max) {
        int minindex = min;
        int maxindex = min;
        for (int i = min; i <= max; i++) {
            if (nums[minindex] > nums[i])
                minindex = i;
            if (nums[maxindex] < nums[i])
                maxindex = i;
        }
        swap(nums[maxindex], nums[max]);
        if (min == maxindex) {
            maxindex = minindex;
        }
        swap(nums[minindex], nums[min]);
        min++;
        max--;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 堆排序

// 堆：下滤操作(大根堆)
void Down(int root) {
    int parent = root;
    int child = 2 * parent + 1;
    // 默认左孩子为较大值
    while (child < nums.size()) {
        if (child + 1 < nums.size() && nums[child] < nums[child + 1])
            child++;
        if (nums[parent] < nums[child]) {
            swap(nums[parent], nums[child]);
            parent = child;
            child = 2 * parent + 1;
        } else {
            break;
        }
    }
}

// 堆排序(升序：建立大根堆)
void HeapSort() {
    for (int i = (int) ((nums.size() - 1) / 2); i >= 0; i--) {
        Down(i);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# 交换排序

# 冒泡排序

void BubbleSort() {
    bool flag = true;
    for (int i = 0; i < nums.size() - 1; i++) {
        for (int j = 0; j < nums.size() - 1 - i; j++) {
            if (nums[j] > nums[j + 1]) {
                swap(nums[j], nums[j + 1]);
                flag = false;
            }
        }
        if (flag)
            break;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13

# 快速排序

Hoare 法： Hoare 版本的单趟排序的基本步骤如下：

选出一个 pivot，一般是最左边或是最右边的。
定义一个 L 和一个 R，L 从左向右走，R 从右向左走。（若选择最左边的数据作为 pivot，则需要 R 先走；若选择最右边的数据作为 pivot，则需要 L 先走）。
在走的过程中，若 R 遇到小于 pivot 的数，则停下，L 开始走，直到 L 遇到一个大于 pivot 的数时，将 L 和 R 的内容交换，R 再次开始走，如此进行下去，直到 L 和 R 最终相遇，此时将相遇点的内容与 pivot 交换即可。

// Hoare法
int PartSort(int left, int right) {
    int start = left;
    int pivot = nums[left];
    while (left < right) {
        while (left < right && nums[right] >= pivot)
            right--;
        while (left < right && nums[left] <= pivot)
            left++;
        if(left < right)
            swap(nums[left++],nums[right--]);
    }
    swap(nums[start],nums[left]);
    return left;
}

// 快速排序(以nums[0]为pivot)
void QuickSort(int left, int right) {
    if (left < right) {
        int index = PartSort(left, right);
        QuickSort(left, index - 1);
        QuickSort(index + 1, right);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

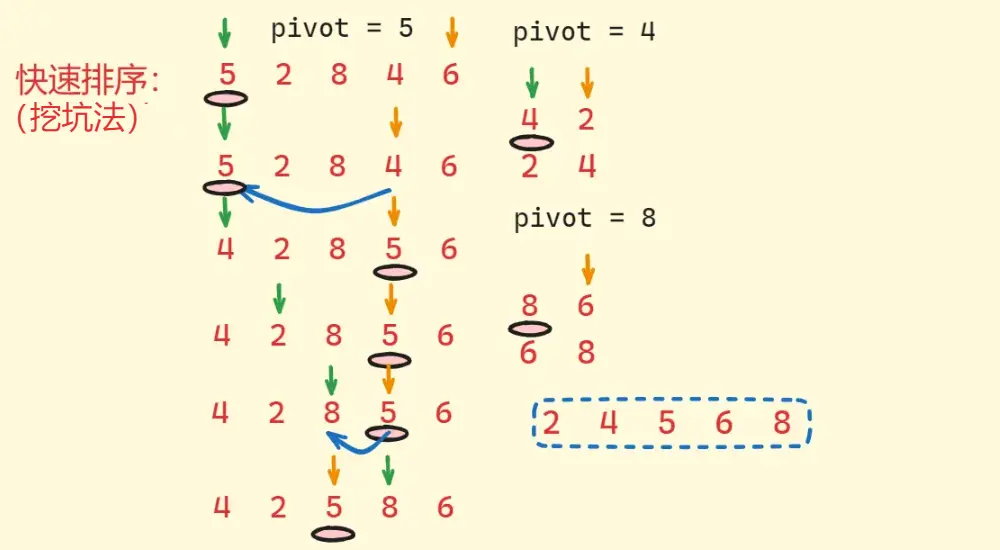
坑位法：

选出一个数据（一般是最左边或是最右边的）作为 pivot，在该数据位置形成一个坑。
还是定义一个 L 和一个 R，L 从左向右走，R 从右向左走。
在走的过程中，若 R 遇到小于 pivot 的数，则将该数抛入坑位，并在此处形成一个坑位，这时 L 再向后走，若遇到大于 pivot 的数，则将其抛入坑位，又形成一个坑位，如此循环下去，直到最终 L 和 R 相遇，这时将 pivot 抛入坑位即可。

// 坑位法
int PartSort(int left, int right) {
    int pivot = nums[left];
    while (left < right) {
        while (left < right && nums[right] >= pivot)
            right--;
        nums[left] = nums[right];
        while (left < right && nums[left] <= pivot)
            left++;
        nums[right] = nums[left];
    }
    nums[left] = pivot;
    return left;
}

// 快速排序(以nums[0]为pivot)
void QuickSort(int left, int right) {
    if (left < right) {
        int index = PartSort(left, right);
        QuickSort(left, index - 1);
        QuickSort(index + 1, right);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

快速排序的优化：

// 坑位法
int QuickPartSort(int left, int right) {
    int pivot = nums[left];
    while (left < right) {
        while (left < right && nums[right] > pivot)
            right--;
        nums[left] = nums[right];
        while (left < right && nums[left] < pivot)
            left++;
        nums[right] = nums[left];
    }
    nums[left] = pivot;
    return left;
}

//三数取中
int GetMidIndex(int left, int right) {
    int mid = left + (right - left) / 2;
    if (nums[mid] > nums[left]) {
        if (nums[mid] < nums[right])
            return mid;
        else if (nums[left] > nums[right])
            return left;
        else
            return right;
    } else {
        if (nums[mid] > nums[right])
            return mid;
        else if (nums[left] > nums[right])
            return right;
        else
            return left;
    }
}

// 快速排序(以nums[0]为pivot)
void QuickSort(int left, int right) {
    if (left < right) {
        int midindex = GetMidIndex(left,right);
        swap(nums[midindex],nums[left]);
        int index = QuickPartSort(left, right);
        QuickSort(left, index - 1);
        QuickSort(index + 1, right);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

# 归并排序

归并排序

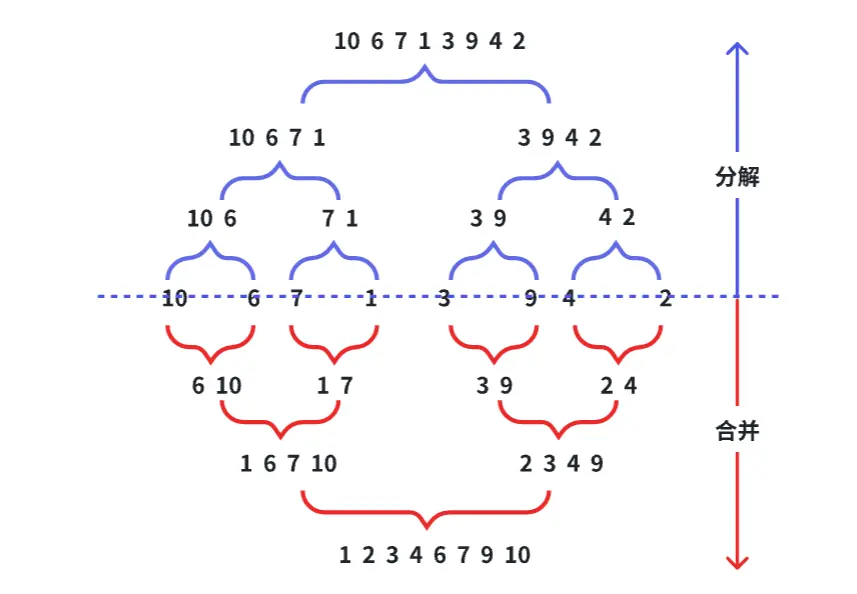
void MergePartSort(int left, int right, vector<int> &temp) {
    if (left >= right)
        return;
    int i = left;
    // 分割
    int mid = left + (right - left) / 2;    // 防止整型溢出
    MergePartSort(left, mid, temp);
    MergePartSort(mid + 1, right, temp);
    // 合并
    int begin1 = left, end1 = mid;
    int begin2 = mid + 1, end2 = right;
    while (begin1 <= end1 && begin2 <= end2) {
        if (nums[begin1] < nums[begin2])
            temp[i++] = nums[begin1++];
        else
            temp[i++] = nums[begin2++];
    }
    while (begin1 <= end1)
        temp[i++] = nums[begin1++];
    while (begin2 <= end2)
        temp[i++] = nums[begin2++];
    // 将临时数组中的排序结果复制回原数组
    for (int j = left; j <= right; ++j) {
        nums[j] = temp[j];
    }
}

// 归并排序
void MergeSort(int left, int right) {
    vector<int> temp(right + 1);
    MergePartSort(left, right, temp);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# 计数排序

// 计数排序
void CountSort() {
    int max = INT_MIN;
    int min = INT_MAX;
    for (int i: nums) {
        if (i > max)
            max = i;
        if (i < min)
            min = i;
    }    vector<int> Countarr(max - min + 1);
    for (int i: nums) {
        Countarr[i - min]++;
    }    int index = 0;
    for (int i = 0; i < Countarr.size(); i++) {
        while (Countarr[i] > 0) {
            nums[index++] = i + min;
            Countarr[i]--;
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# 总结

排序方法	平均情况	最好情况	最坏情况	辅助空间	稳定性
插入排序	O(n²)	O(n)	O(n²)	O(1)	稳定
希尔排序	O(nlogn)~O(n²)	O(n^1.3)	O(n²)	O(1)	不稳定
选择排序	O(n²)	O(n²)	O(n²)	O(1)	不稳定
堆排序	O(nlogn)	O(nlogn)	O(nlogn)	O(1)	不稳定
冒泡排序	O(n²)	O(n)	O(n²)	O(1)	稳定
快速排序	O(nlogn)	O(nlogn)	O(n²)	O(logn)~O(n)	不稳定
归并排序	O(nlogn)	O(nlogn)	O(nlogn)	O(n)	稳定

上次更新: 2025/11/11, 22:03:54

← 堆搜索二叉树→