堆（Heap）是一种特殊的树状数据结构，通常以一种特定的方式组织其节点值。最常见的是二叉堆，它具有以下性质：

1. 完全性：堆总是一棵完全二叉树，意味着除了最后一层外，所有层次都被节点填满，并且最后一层的节点尽可能靠左排列。

2. 堆序性：根据堆的类型，节点与其子节点之间满足一定的顺序关系。

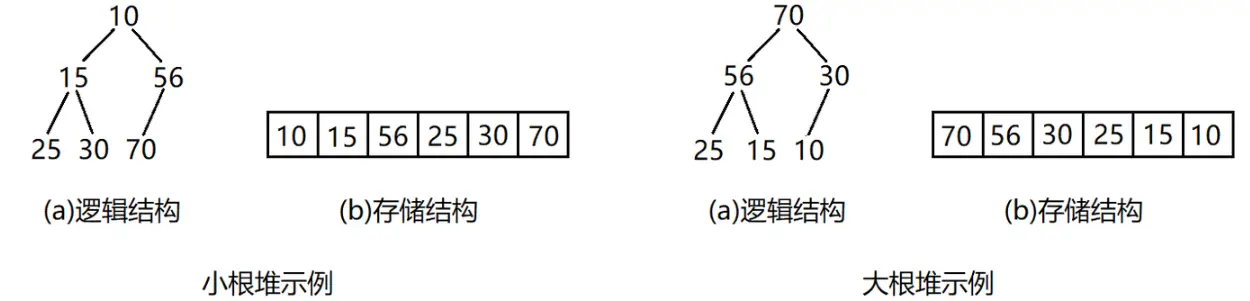
   • 在最大堆（Max-Heap）中，每个节点的值都大于或等于其子节点的值，因此堆顶（根节点）总是存储最大值。

   • 在最小堆（Min-Heap）中，每个节点的值都小于或等于其子节点的值，所以堆顶是整个堆中的最小值。

堆常用于实现优先队列，因为它们可以高效地找到最大或最小元素（取决于堆的类型），并且在插入新元素或移除根节点后能够快速恢复堆属性。

如果有一个关键码的集合K={k0,k1,k2,…,kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足ki<=k2i+1且ki<=k2i+2（或满足ki>=k2i+1且ki>=k2i+2），其中i=0,1,2,…，则称该集合为堆。

技巧：

1. 父节点下标是i，左孩子：2 * i + 1,右孩子：2 * i + 2

2. 孩子的下标是i，父亲的下标：(i - 1) / 2

向下调整算法

当我们想要构建堆的时候，可以用到堆的向下调整算法：

使用向下调整算法需要满足一个前提：

• 若想将其调整为小堆，那么根结点的左右子树必须都为小堆
• 若想将其调整为大堆，那么根结点的左右子树必须都为大堆

向下调整算法的步骤：（以建小堆为例）：

1. 从根结点处开始，选出左右孩子中值较小的孩子。

2. 让小的孩子与其父亲进行比较。

3. 若小的孩子比父亲还小，则该孩子与其父亲的位置进行交换。并将原来小的孩子的位置当成父亲继续向下进行调整，直到调整到叶子结点为止；否则，则不需处理了。

向上调整算法

当我们在一个堆的末尾插入一个数据后，需要对堆进行调整，使其仍然是一个堆，这时需要用到堆的向上调整算法

向上调整算法的步骤：（以建小堆为例）：

1. 将目标结点与其父结点比较。

2. 若目标结点的值比其父结点的值小，则交换目标结点与其父结点的位置，并将原目标结点的父结点当作新的目标结点继续进行向上调整。若目标结点的值比其父结点的值大，则停止向上调整，此时该树已经是小堆了。

堆的插入

数据插入时是插入到数组的末尾，即树形结构的最后一层的最后一个结点，所以插入数据后我们需要运用堆的向上调整算法对堆进行调整，使其在插入数据后仍然保持堆的结构。

堆的删除

方法：堆的删除，删除的是堆顶的元素，但是这个删除过程可并不是直接删除堆顶的数据，而是先将堆顶的数据与最后一个结点的位置交换，然后再删除最后一个结点，再对堆进行一次向下调整。

原因：我们若是直接删除堆顶的数据，那么原堆后面数据的父子关系就全部打乱了，需要全体重新建堆。若是用上述方法，那么只需要对堆进行一次向下调整即可，因为此时根结点的左右子树都是小堆，我们只需要在根结点处进行一次向下调整即可，并且要忽略被替换下的堆顶元素。

小堆的实现

// 构建小堆
class Heap {
private:
    vector<int> v;
    int size;
    // 向下调整算法
    void adjustdown(int root, int n);

    // 向上调整算法
    void adjustup(int child);

public:
    explicit Heap(vector<int> &nums) : v(nums), size(v.size()) {}

    // 构建小堆
    void initHeap(int n);

    // 增
    void push(int x);

    // 删
    void pop();

    // 打印数组
    void printv();

    // 堆顶数据
    int top();
    // 判空
    bool empty() const;

};


// 小堆的向下调整算法:前提是左右子堆是小堆，来构建小堆
void Heap::adjustdown(int root, int n) {
    int parent = root;
    int child = 2 * parent + 1;  // 子堆中的较小值(默认左子树较小)
    while (child < n) {
        if (child + 1 < n && v[child] > v[child + 1])
            child++;
        if (v[parent] > v[child]) {
            swap(v[parent], v[child]);
            parent = child;
            child = 2 * parent + 1;
        } else
            break;
    }
}

void Heap::adjustup(int child) {
    while (child > 0) {
        int parent = (child - 1) / 2;
        if (v[child] < v[parent]) {
            swap(v[child], v[parent]);
            child = parent;
        } else {
            break;
        }
    }
}

void Heap::initHeap(int n) {
    for (int i = (int) ((n - 2) / 2); i >= 0; i--) {
        adjustdown(i, n);
    }
}

void Heap::push(int x) {
    v.push_back(x);
    size++;
    adjustup(size - 1);
}

// 删除堆顶元素
void Heap::pop() {
    if(size <= 0) {
        cout << "当前堆中无数据！" << endl;
        return;
    }
    size--;
    swap(v[0],v[v.size() - 1]);
    adjustdown(0,size - 1);
}

void Heap::printv() {
    for (int i = 0;i < size;i++) {
        cout << v[i] << " ";
    }
}

int Heap::top() {
    return v[0];
}

bool Heap::empty() const {
    return size == 0;
}


int main() {
    vector<int> v = {100, 3, 5, 7, 4, 2, 11};
    Heap heap(v);
    heap.initHeap(v.size());
    heap.push(10000);
    heap.push(1);
    heap.push(6);
    heap.printv();
    cout << endl;
    heap.pop();
    heap.printv();
    
    return 0;
}

构建大堆与之类似，只需要修改下调和上调两个过程即可

TopK问题

描述：

输入数组arr，找出其中最大的k个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最大的4个数字是5、6、7、8。

示例一：  输入：arr = [3,2,1], k = 2

输出：[3,2]或者[2,3]

示例二：  输入：arr = [0,1,2,1], k = 1

输出：[2]

方法：

1. 先将数组的前k个数建为小堆。就是最大的k个数了
2. 将数组剩下的N—k个数依次与堆顶元素进行 比较，若比堆顶元素大，则将堆顶元素替换为该元素，然后再进行一次向下调整，使其仍为小堆。
3. 最后，堆里面的k个数就是最大的k个数

代码：

void topk(vector<int>& arr,int k) {  
    vector<int> top(arr.begin(),arr.begin() + k);  
    Heap temp(top);  
    for(int i = k;i < arr.size();i++) {  
        if(arr[i] > temp.top()) {  
            temp.v[0] = arr[i];  
            adjustdown(0,k);  
        }    
    }    
    temp.printv();  
}

# from cen

---