引入

二叉搜索树虽然可以提高我们查找数据的效率，但如果插入二叉搜索树的数据是有序或接近有序的，此时二叉搜索树会退化为单支树，在单支树当中查找数据相当于在单链表当中查找数据，效率是很低下的。因此，引入了平衡二叉树。

AVL树可以是一棵具有以下性质的一棵二叉搜索树：

• 树的左右子树都是AVL树
• 树的左右子树高度之差（简称平衡因子）的绝对值不超过1（-1/0/1）

插入数据

三个步骤：

1. 按照搜索二叉树的插入方法，找到待插入位置
2. 找到待插入位置后，将待插入结点插入到树中
3. 更新平衡因子，如果出现不平衡，则需要进行必要的旋转

• 插入数据：

若待插入结点的值小于根结点的值，则需要将结点插入到左子树当中 若待插入结点的值大于根结点的值，则需要将结点插入到右子树当中 若待插入结点的值等于根结点的值，则插入结点失败

• 更新平衡因子：

插入一个结点后，该结点的祖先结点的平衡因子需要更新。

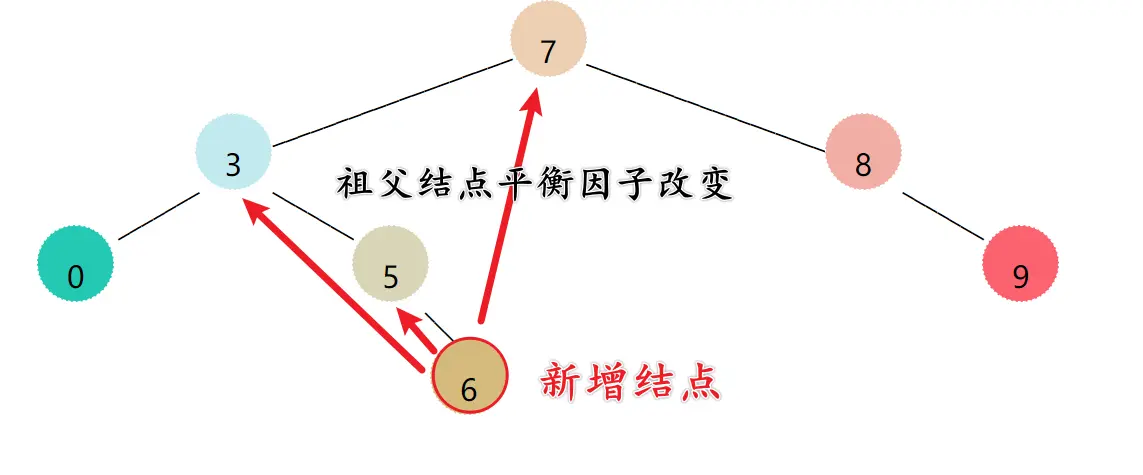
更新规则：

• 新增结点在parent的右边，parent的平衡因子 ++
• 新增结点在parent的左边，parent的平衡因子 −−

每更新完一个结点的平衡因子后，都需要进行以下判断：

• 如果parent的平衡因子等于-1或者1，表明还需要继续往上更新平衡因子
• 如果parent的平衡因子等于0，表明无需继续往上更新平衡因子了
• 如果parent的平衡因子等于-2或者2，表明此时以parent结点为根结点的子树已经不平衡了，需要进行旋转处理

旋转处理

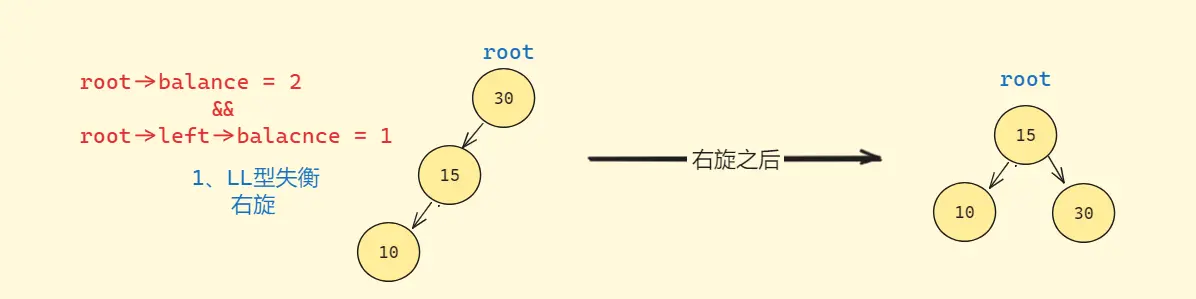
右单旋

当parent的平衡因子为2，cur的平衡因子为1时，进行右单旋

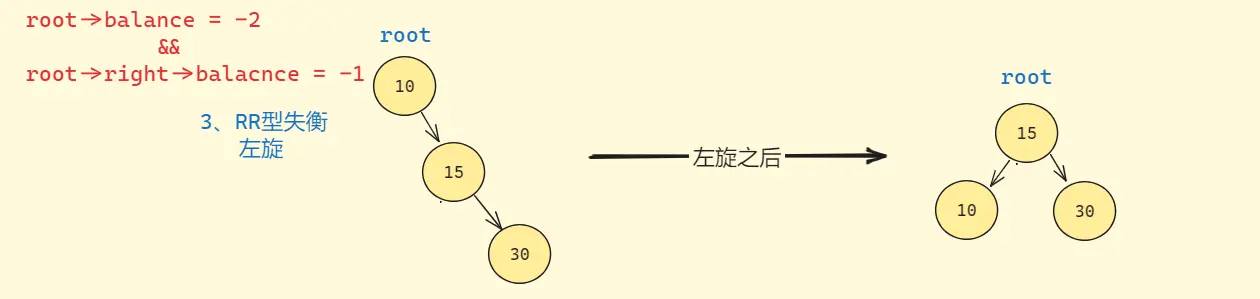
左单旋

当parent的平衡因子为-2，cur的平衡因子为-1时，进行左单旋

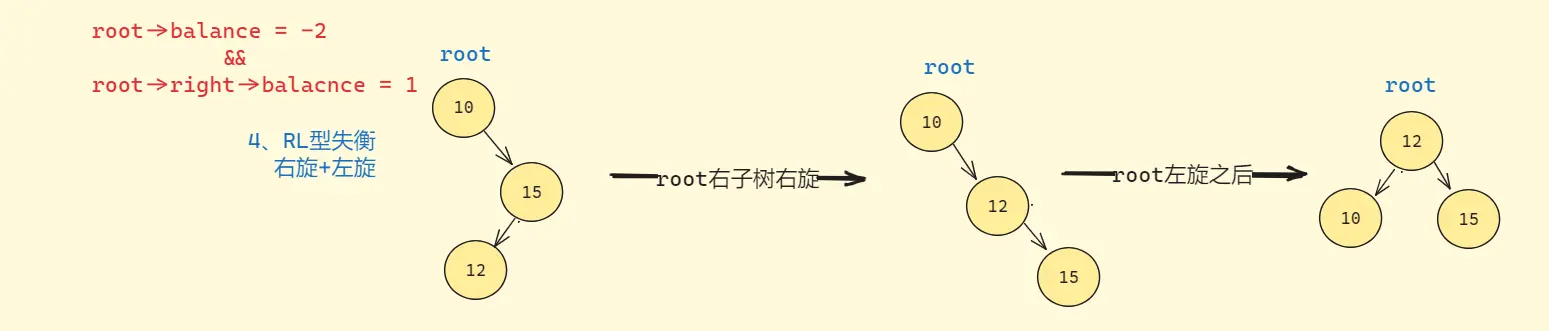
右左双旋

当parent的平衡因子为-2，cur的平衡因子为1时，进右左双旋

左右双旋

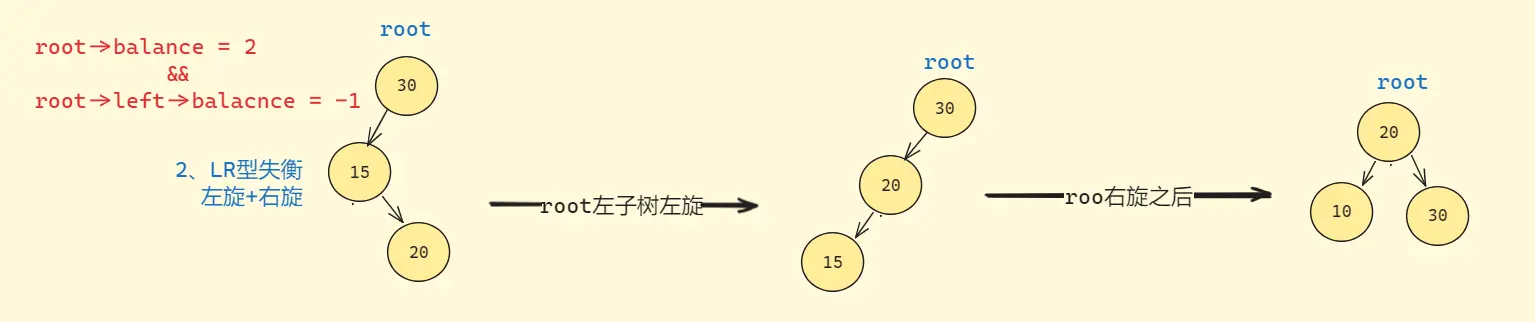
当parent的平衡因子为2，cur的平衡因子为-1时，进行左右双旋

总结

AVL树是一棵绝对平衡的二叉搜索树，其要求每个结点的左右子树高度差的绝对值都不超过1，这样可以保证查询时高效的时间复杂度，即O(logn)。但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多。 因此，如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的（即不会改变），可以考虑AVL树，但当一个结构经常需要被修改时，AVL树就不太适合了。